Какими свойствами обладает параллелограмм. Параллелограмм и его свойства

Параллелограмм – это четырехугольник, у которого стороны попарно параллельны.

В этой фигуре противоположные стороны и углы равны между собой. Диагонали параллелограмма пересекаются в одной точке и делятся ей пополам. Формулы площади параллелограмма позволяют найти значение через стороны, высоту и диагонали. Параллелограмм также может быть представлен в частных случаях. Ими считаются прямоугольник, квадрат и ромб.
Для начала рассмотрим пример расчета площади параллелограмма по высоте и стороне, к которой она опущена.

Этот случай считается классическим и не требует дополнительного разбирательства. Лучше рассмотрим формулу вычисления площади через две стороны и угол между ними. Этот же способ применяется в расчете . Если даны стороны и угол между ними, то площадь рассчитывается так:

Допустим, дан параллелограмм со сторонами a = 4 см, b = 6 см. Угол между ними α = 30°. Найдем площадь:

Площадь параллелограмма через диагонали

Формула площади параллелограмма через диагонали позволяет быстро найти значение.
Для вычислений понадобится величина угла, расположенного между диагоналями.

Рассмотрим пример расчета площади параллелограмма через диагонали. Пусть дан параллелограмм с диагоналями D = 7 см, d = 5 см. Угол, лежащий между ними α =30°. Подставим данные в формулу:

Пример расчета площади параллелограмма через диагональ дал нам прекрасный результат – 8,75.

Зная формулу площади параллелограмма через диагональ можно решать множество интересных задач. Давайте рассмотрим одну из них.

Задача: Дан параллелограмм с площадью 92 кв. см. Точка F расположена на середине его стороны ВС . Давайте найдем площадь трапеции ADFB , которая будет лежать в нашем параллелограмме. Для начала нарисуем все, что получили по условиям.
Приступаем к решению:

По нашим условиям ah =92, а соответственно, площадь нашей трапеции будет равняться

Это четырёхугольник, противоположные стороны которого попарно параллельны.

Свойство 1 . Любая диагональ параллелограмма делит его на два равных треугольника.

Доказательство . По II признаку (накрест лежащие углы и общая сторона).

Теорема доказана .

Свойство 2 . В параллелограмме противолежащие стороны равны, противолежащие углы равны.

Доказательство .
Аналогично,

Теорема доказана .

Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.

Доказательство .

Теорема доказана .

Свойство 4 . Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. - вершину - два равнобедренных?-ка).

Доказательство .

Теорема доказана .

Свойство 5 . В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.

Доказательство .

Теорема доказана .

Свойство 6 . Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.

Доказательство .

Теорема доказана .

Свойство 7 . Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.

Доказательство .

Теорема доказана .

Построение биссектрисы угла. Свойства биссектрисы угла треугольника.

1) Построить произвольный луч DE.

2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.

3) F и G - точки пересечения окружности со сторонами данного угла, H - точка пересечения окружности с построенным лучом

Построить окружность с центром в точке H и радиусом, равным FG.

5) I - точка пересечения окружностей построенного луча.

6) Провести прямую через вершину и I.

IDH - требуемый угол.
)

Свойство 1 . Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.

Доказательство . Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.

Доказательство

Первым делом проведем диагональ AC . Получаются два треугольника: ABC и ADC .

Так как ABCD — параллелограмм, то справедливо следующее:

AD || BC \Rightarrow \angle 1 = \angle 2 как лежащие накрест.

AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.

Следовательно, \triangle ABC = \triangle ADC (по второму признаку: и AC — общая).

И, значит, \triangle ABC = \triangle ADC , то AB = CD и AD = BC .

Доказано!

2. Противоположные углы тождественны.

Доказательство

Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4 . Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4 . Учитывая, что \triangle ABC = \triangle ADC получаем \angle A = \angle C , \angle B = \angle D .

Доказано!

3. Диагонали разделены пополам точкой пересечения.

Доказательство

Проведем еще одну диагональ.

По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD . Еще раз отметим накрест лежащие равные углы.

Таким образом видно, что \triangle AOB = \triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов \angle 2 и \angle 1 ) и AO = OC (напротив углов \angle 3 и \angle 4 соответственно).

Доказано!

Признаки параллелограмма

Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.

Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?» . То есть, как узнать, что заданная фигура это параллелограмм.

1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.

AB = CD ; AB || CD \Rightarrow ABCD — параллелограмм.

Доказательство

Рассмотрим подробнее. Почему AD || BC ?

\triangle ABC = \triangle ADC по свойству 1 : AB = CD , AC — общая и \angle 1 = \angle 2 как накрест лежащие при параллельных AB и CD и секущей AC .

Но если \triangle ABC = \triangle ADC , то \angle 3 = \angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (\angle 3 и \angle 4 - накрест лежащие тоже равны).

Первый признак верен.

2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.

AB = CD , AD = BC \Rightarrow ABCD — параллелограмм.

Доказательство

Рассмотрим данный признак. Еще раз проведем диагональ AC .

По свойству 1 \triangle ABC = \triangle ACD .

Из этого следует, что: \angle 1 = \angle 2 \Rightarrow AD || BC и \angle 3 = \angle 4 \Rightarrow AB || CD , то есть ABCD — параллелограмм.

Второй признак верен.

3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны.

\angle A = \angle C , \angle B = \angle D \Rightarrow ABCD — параллелограмм.

Доказательство

2 \alpha + 2 \beta = 360^{\circ} (поскольку ABCD — четырехугольник, а \angle A = \angle C , \angle B = \angle D по условию).

Получается, \alpha + \beta = 180^{\circ} . Но \alpha и \beta являются внутренними односторонними при секущей AB .

И то, что \alpha + \beta = 180^{\circ} говорит и о том, что AD || BC .

При этом \alpha и \beta — внутренние односторонние при секущей AD . И это значит AB || CD .

Третий признак верен.

4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.

AO = OC ; BO = OD \Rightarrow параллелограмм.

Доказательство

BO = OD ; AO = OC , \angle 1 = \angle 2 как вертикальные \Rightarrow \triangle AOB = \triangle COD , \Rightarrow \angle 3 = \angle 4 , и \Rightarrow AB || CD .

Аналогично BO = OD ; AO = OC , \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 , и \Rightarrow AD || BC .

Четвертый признак верен.

Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых

Свойства параллелограмма: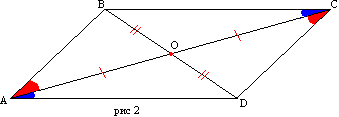
Теорема 22. Противоположные стороны параллелограма равны.
Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠ САВ=∠ АСD, ∠ АСВ=∠ DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Теорема 23. Противоположные углы параллелограмма равны: ∠ А=∠ С и ∠ В=∠ D.
Равенство первой пары идет из равенства треугольников АВD и CBD, а второй - АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠ ОАD=∠ ОСВ и ∠ ОDА=∠ ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.

Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.
Пусть ∠ А=∠ С и ∠ В=∠ D. Т.к. ∠ А+∠ В+∠ С+∠ D=360 о, то ∠ А+∠ В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.
Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник - параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.

В геометрии рассматривают частные случаи параллелограмма.

При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:

1. Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
2. Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
3. Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
5. Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними

Рассмотрим задачи, при решении которых используются данные свойства.

Задача 1.

Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.

Решение.

1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.

2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.

3. АD = АМ + МD = 7 см.

4. Периметр АВСD = 20 см.

Ответ. 20 см.

Задача 2.

В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.

Решение.

1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.

2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD. ВЕ = СF. Следовательно, прямая ВС || AD. (*)

3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.

4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)

5. Из условий (*), (**) вытекает – АВСD параллелограмм.

Ответ. Доказано. АВСD – параллелограмм.

Задача 3.

На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О; <ВМD = 95 о,