Fördelningstätheten för den slumpmässiga variabeln x ges. Förväntning på en kontinuerlig stokastisk variabel

………………………………………………………

Аn - slumpvariabel X har tagit värdet An.

Det är uppenbart att summan av händelser A1 A2, . , An är en tillförlitlig händelse, eftersom den slumpmässiga variabeln måste ta minst ett av värdena x1, x2, xn.

Därför P (A1 È A2 È . È An) = 1.

Dessutom är händelserna A1, A2, ., An inkonsekventa, eftersom en slumpvariabel under ett enda experiment bara kan ta ett av värdena x1, x2, ., xn. Genom att använda additionssatsen för inkompatibla händelser får vi

P(A1)+P(A2)+ .+P(An)=1,

dvs pl+p2+. +pn = 1, eller kort sagt,

Därför måste summan av alla tal som finns i den andra raden i Tabell 1, som ger fördelningslagen för den slumpmässiga variabeln X, vara lika med ett.

EXEMPEL 1. Låt slumpvariabeln X vara antalet poäng som erhålls när man kastar en tärning. Hitta distributionslagen (i tabellform).

Slumpvariabeln X tar värden

x1=1, x2=2, …, x6=6

med sannolikheter

р1= р2 = … = р6 =

Fördelningslagen ges av tabellen:

Tabell 2

EXEMPEL 2. Binomialfördelning. Låt oss betrakta en slumpvariabel X - antalet förekomster av händelse A i en serie oberoende experiment, i var och en av vilka A inträffar med sannolikhet p.

Den slumpmässiga variabeln X kan uppenbarligen ta ett av följande värden:

0, 1, 2, ., k, ., n.

Sannolikheten för händelsen att den slumpmässiga variabeln X tar ett värde lika med k bestäms av Bernoullis formel:

Рn(k)= där q=1-р.

Denna fördelning av en slumpvariabel kallas en binomialfördelning eller Bernoullifördelning. Bernoulli-fördelningen är helt specificerad av två parametrar: antalet n av alla experiment och sannolikheten p med vilken en händelse inträffar i varje enskilt experiment.

Villkoret för binomialfördelningen har formen:

För att bevisa giltigheten av denna jämlikhet räcker det med identiteten

(q+px)n=

sätt x=1.

EXEMPEL 3. Poissonfördelning. Detta är namnet på formens sannolikhetsfördelning:

Р(k)= .

Den bestäms av en enda (positiv) parameter a. Om ξ är en slumpvariabel med en Poisson-fördelning, då är motsvarande parameter a medelvärdet för denna slumpvariabel:

a=Mξ=, där M är den matematiska förväntan.

Den slumpmässiga variabeln är:

EXEMPEL 4. Exponentiell fördelning.

Om tiden är en slumpmässig variabel, låt oss beteckna den med τ, så att

där 0<λ=const, t ³ 0, причем, если t=0, то P(t)=0.

Medelvärdet för den slumpmässiga variabeln t är:

Fördelningstätheten har formen:

4) Normalfördelning

Låta vara oberoende, identiskt fördelade slumpvariabler och låt Om termerna är tillräckligt små och talet n är tillräckligt stort, om för n à ∞ den matematiska förväntan av stokastisk variabel Mξ och variansen Dξ lika med Dξ=M(ξ–Mξ)2 är sådana att Mξ~a, Dξ ~σ2, alltså

- normal eller gaussisk fördelning

.

5) Geometrisk fördelning. Låt oss beteckna med ξ antalet försök som föregår början av den första "framgången". Om vi ​​antar att varje test varar en tidsenhet, så kan vi betrakta ξ som väntetiden tills den första "framgången". Fördelningen ser ut så här:

Р(k)=p(1-p)k, (k=0, 1, 2) p>0

6) Hypergeometrisk fördelning.

Det finns N objekt, bland vilka n är "speciella objekt". Bland alla objekt väljs k-objekt slumpmässigt ut. Hitta sannolikheten att det bland de valda objekten är lika med r - "speciella objekt". Fördelningen ser ut så här:

7) Pascalfördelning.

Låt x vara det totala antalet "misslyckanden" som föregår ankomsten av den första "framgången". Fördelningen ser ut så här:

Distributionsfunktionen har formen:

Ekvisannolikhetsfördelning innebär att den slumpmässiga variabeln x kan ta vilket värde som helst på intervallet med lika sannolikhet. Fördelningstätheten beräknas som

Graferna för distributionstätheten och fördelningsfunktionen presenteras nedan.

Innan du förklarar begreppet "vitt brus", är det nödvändigt att ge ett antal definitioner.

En slumpmässig funktion är en funktion av ett icke-slumpmässigt argument t, som för varje fast värde i argumentet är en slumpvariabel. Till exempel, om U är en slumpvariabel, då är funktionen X(t)=t2U slumpmässig.

Tvärsnittet av en slumpmässig funktion är en slumpmässig variabel som motsvarar ett fast värde på argumentet för slumpfunktionen. Således kan en slumpmässig funktion betraktas som en uppsättning slumpvariabler (X(t)), beroende på parametern t.

Slumpvariabel är en variabel som kan anta vissa värden beroende på olika omständigheter, och slumpmässig variabel kallas kontinuerlig , om det kan ta vilket värde som helst från ett begränsat eller obegränsat intervall. För en kontinuerlig slumpmässig variabel är det omöjligt att ange alla möjliga värden, så vi anger intervall av dessa värden som är associerade med vissa sannolikheter.

Exempel på kontinuerliga slumpvariabler inkluderar: diametern på en del som slipas till en given storlek, höjden på en person, flygräckvidden för en projektil, etc.

Eftersom för kontinuerliga slumpvariabler funktionen F(x), Till skillnad från diskreta slumpvariabler, har inga hopp någonstans, då är sannolikheten för ett individuellt värde på en kontinuerlig slumpvariabel noll.

Detta betyder att för en kontinuerlig slumpvariabel är det ingen mening att tala om sannolikhetsfördelningen mellan dess värden: var och en av dem har noll sannolikhet. Men på sätt och vis, bland värdena för en kontinuerlig slumpmässig variabel finns det "mer och mindre sannolika". Till exempel skulle knappast någon tvivla på att värdet av en slumpmässig variabel - höjden på en slumpmässigt påträffad person - 170 cm - är mer sannolikt än 220 cm, även om båda värdena kan förekomma i praktiken.

Fördelningsfunktion av en kontinuerlig stokastisk variabel och sannolikhetstäthet

Som en distributionslag som är vettig endast för kontinuerliga slumpvariabler introduceras begreppet distributionstäthet eller sannolikhetstäthet. Låt oss närma oss det genom att jämföra betydelsen av fördelningsfunktionen för en kontinuerlig slumpvariabel och för en diskret slumpvariabel.

Så fördelningsfunktionen för en slumpvariabel (både diskret och kontinuerlig) eller integrerad funktion kallas en funktion som bestämmer sannolikheten att värdet av en slumpvariabel X mindre än eller lika med gränsvärdet X.

För en diskret slumpvariabel vid punkterna för dess värden x1 , x 2 , ..., x jag,... massor av sannolikheter är koncentrerade sid1 , sid 2 , ..., sid jag,..., och summan av alla massor är lika med 1. Låt oss överföra denna tolkning till fallet med en kontinuerlig stokastisk variabel. Låt oss föreställa oss att en massa lika med 1 inte är koncentrerad till enskilda punkter, utan kontinuerligt "smetad" längs abskissaxeln Åh med viss ojämn densitet. Sannolikheten för att en stokastisk variabel faller inom valfritt område Δ x kommer att tolkas som massan per sektion, och medeldensiteten vid den sektionen som förhållandet mellan massa och längd. Vi har precis introducerat ett viktigt begrepp inom sannolikhetsteorin: distributionstäthet.

Sannolikhetstäthet f(x) av en kontinuerlig slumpvariabel är derivatan av dess fördelningsfunktion:

.

Genom att känna till densitetsfunktionen kan du hitta sannolikheten att värdet av en kontinuerlig slumpvariabel tillhör det slutna intervallet [ a; b]:

sannolikheten att en kontinuerlig stokastisk variabel X kommer att ta vilket värde som helst från intervallet [ a; b], är lika med en viss integral av dess sannolikhetstäthet som sträcker sig från a innan b:

.

I det här fallet den allmänna formeln för funktionen F(x) sannolikhetsfördelning av en kontinuerlig stokastisk variabel, som kan användas om densitetsfunktionen är känd f(x) :

.

Sannolikhetstäthetsgrafen för en kontinuerlig slumpvariabel kallas dess fördelningskurva (figur nedan).

Area av en figur (skuggad i figuren) avgränsad av en kurva, raka linjer ritade från punkter a Och b vinkelrät mot x-axeln och axeln Åh, visar grafiskt sannolikheten att värdet av en kontinuerlig slumpvariabel X ligger inom intervallet för a innan b.

Egenskaper för sannolikhetstäthetsfunktionen för en kontinuerlig stokastisk variabel

1. Sannolikheten för att en slumpvariabel tar något värde från intervallet (och arean av figuren som begränsas av funktionens graf f(x) och axel Åh) är lika med en:

2. Sannolikhetstäthetsfunktionen kan inte ta negativa värden:

och utanför existensen av fördelningen är dess värde noll

Fördelningstäthet f(x), samt distributionsfunktionen F(x), är en av formerna för distributionslagen, men till skillnad från fördelningsfunktionen är den inte universell: distributionstätheten existerar endast för kontinuerliga slumpvariabler.

Låt oss nämna de två viktigaste typerna av distribution av en kontinuerlig stokastisk variabel i praktiken.

Om distributionstätheten funktion f(x) kontinuerlig stokastisk variabel i något ändligt intervall [ a; b] tar ett konstant värde C, och utanför intervallet tar ett värde lika med noll, då detta fördelningen kallas enhetlig .

Om grafen för fördelningsdensitetsfunktionen är symmetrisk om mitten, koncentreras medelvärdena nära mitten, och när man flyttar bort från centrum samlas de som skiljer sig mer från genomsnittet (grafen för funktionen liknar en sektion av en klocka), sedan detta distribution kallas normal .

Exempel 1. Sannolikhetsfördelningsfunktionen för en kontinuerlig stokastisk variabel är känd:

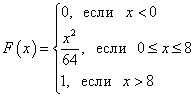
Hitta funktion f(x) sannolikhetstäthet för en kontinuerlig stokastisk variabel. Konstruera grafer för båda funktionerna. Hitta sannolikheten för att en kontinuerlig slumpvariabel tar vilket värde som helst i intervallet från 4 till 8: .

Lösning. Vi får sannolikhetstäthetsfunktionen genom att hitta derivatan av sannolikhetsfördelningsfunktionen:

Graf över en funktion F(x) - parabel:

Graf över en funktion f(x) - hetero:

Låt oss ta reda på sannolikheten för att en kontinuerlig slumpvariabel kommer att ta vilket värde som helst i intervallet från 4 till 8:

Exempel 2. Sannolikhetstäthetsfunktionen för en kontinuerlig stokastisk variabel ges som:

Beräkna koefficient C. Hitta funktion F(x) sannolikhetsfördelning av en kontinuerlig stokastisk variabel. Konstruera grafer för båda funktionerna. Hitta sannolikheten att en kontinuerlig slumpvariabel kommer att ta vilket värde som helst i intervallet från 0 till 5: .

Lösning. Koefficient C vi finner, med hjälp av egenskap 1 i sannolikhetstäthetsfunktionen:

Således är sannolikhetstäthetsfunktionen för en kontinuerlig slumpvariabel:

Genom att integrera hittar vi funktionen F(x) sannolikhetsfördelningar. Om x < 0 , то F(x) = 0 . Om 0< x < 10 , то

.

x>10 alltså F(x) = 1 .

Således är den fullständiga posten för sannolikhetsfördelningsfunktionen:

Graf över en funktion f(x) :

Graf över en funktion F(x) :

Låt oss ta reda på sannolikheten för att en kontinuerlig slumpvariabel kommer att ta vilket värde som helst i intervallet från 0 till 5:

Exempel 3. Sannolikhetstäthet för en kontinuerlig stokastisk variabel X ges av jämlikheten, och . Hitta koefficient A, sannolikheten att en kontinuerlig stokastisk variabel X kommer att ta vilket värde som helst från intervallet ]0, 5[, fördelningsfunktionen för en kontinuerlig slumpvariabel X.

Lösning. Genom villkor kommer vi fram till jämlikhet

Därför, varifrån. Så,

.

Nu finner vi sannolikheten att en kontinuerlig stokastisk variabel X kommer att ta vilket värde som helst från intervallet ]0, 5[:

Nu får vi fördelningsfunktionen för denna slumpvariabel:

Exempel 4. Hitta sannolikhetstätheten för en kontinuerlig stokastisk variabel X, som endast tar icke-negativa värden, och dess fördelningsfunktion .

Övning 1. Fördelningstätheten för en kontinuerlig slumpvariabel X har formen:
Hitta:
a) parameter A;
b) fördelningsfunktion F(x);
c) sannolikheten för att en stokastisk variabel X faller in i intervallet;
d) matematisk förväntan MX och varians DX.
Rita en graf över funktionerna f(x) och F(x).

Uppgift 2. Hitta variansen för den slumpmässiga variabeln X som ges av integralfunktionen.

Uppgift 3. Hitta den matematiska förväntan av den slumpmässiga variabeln X givet fördelningsfunktionen.

Uppgift 4. Sannolikhetstätheten för någon stokastisk variabel ges enligt följande: f(x) = A/x 4 (x = 1; +∞)
Hitta koefficient A, fördelningsfunktion F(x), matematisk förväntan och varians, samt sannolikheten att den slumpmässiga variabeln tar ett värde i intervallet. Rita grafer f(x) och F(x).

Uppgift. Fördelningsfunktionen för någon kontinuerlig stokastisk variabel ges enligt följande:

Bestäm parametrarna a och b, hitta ett uttryck för sannolikhetstätheten f(x), matematisk förväntan och varians, samt sannolikheten att den slumpmässiga variabeln tar ett värde i intervallet. Rita grafer av f(x) och F(x).

Låt oss hitta fördelningsdensitetsfunktionen som en derivata av fördelningsfunktionen.
F′=f(x)=a
Att veta att vi kommer att hitta parameter a:

eller 3a=1, varav a = 1/3
Vi hittar parametern b från följande egenskaper:
F(4) = a*4 + b = 1
1/3*4 + b = 1 varav b = -1/3
Därför har fördelningsfunktionen formen: F(x) = (x-1)/3

Förväntat värde.


Dispersion.

1 / 9 4 3 - (1 / 9 1 3) - (5 / 2) 2 = 3 / 4
Låt oss hitta sannolikheten för att den slumpmässiga variabeln kommer att ta ett värde i intervallet
P(2< x< 3) = F(3) – F(2) = (1/3*3 - 1/3) - (1/3*2 - 1/3) = 1/3

Exempel nr 1. Sannolikhetsfördelningstätheten f(x) för en kontinuerlig stokastisk variabel X ges. Nödvändig:

1. Bestäm koefficient A.
2. hitta fördelningsfunktionen F(x) .
3. Konstruera schematiskt grafer av F(x) och f(x).
4. hitta den matematiska förväntan och variansen för X.
5. hitta sannolikheten att X tar ett värde från intervallet (2;3).

f(x) = A*sqrt(x), 1 ≤ x ≤ 4.
Lösning:

Den slumpmässiga variabeln X specificeras av fördelningsdensiteten f(x):

Låt oss hitta parameter A från villkoret:



eller
14/3*A-1 = 0
Var,
A = 3/14

Fördelningsfunktionen kan hittas med formeln.

SLUMPMÄSSIGA VARIABLER

Exempel 2.1. Slumpmässigt värde X ges av distributionsfunktionen

Hitta sannolikheten att som ett resultat av testet X kommer att ta värden som finns i intervallet (2,5; 3,6).

Lösning: X i intervallet (2.5; 3.6) kan bestämmas på två sätt:

Exempel 2.2. Vid vilka parametervärden A Och I fungera F(x) = A + Be - x kan vara en fördelningsfunktion för icke-negativa värden av en slumpvariabel X.

Lösning: Eftersom alla möjliga värden för den slumpmässiga variabeln X tillhöra intervallet , då för att funktionen ska vara en fördelningsfunktion för X, måste fastigheten vara uppfylld:

.

Svar: .

Exempel 2.3. Slumpvariabeln X specificeras av fördelningsfunktionen

Hitta sannolikheten att, som ett resultat av fyra oberoende tester, värdet X exakt 3 gånger kommer att ta ett värde som hör till intervallet (0,25;0,75).

Lösning: Sannolikhet att träffa ett värde X i intervallet (0,25;0,75) finner vi att använda formeln:

Exempel 2.4. Sannolikheten för att bollen träffar korgen med ett skott är 0,3. Gör upp en fördelningslag för antalet träffar med tre kast.

Lösning: Slumpmässigt värde X– antalet träffar i korgen med tre skott – kan ta följande värden: 0, 1, 2, 3. Sannolikheter för att X

X:

Exempel 2.5. Två skyttar skjuter vardera ett skott mot ett mål. Sannolikheten för att den första skytten träffar den är 0,5, den andra - 0,4. Gör upp en distributionslag för antalet träffar på ett mål.

Lösning: Låt oss hitta fördelningens lag för en diskret slumpvariabel X– antal träffar på målet. Låt händelsen vara den första skytten som träffar målet, och låt den andra skytten träffa målet, respektive vara deras missar.

Låt oss komponera lagen om sannolikhetsfördelning för SV X:

Exempel 2.6. Tre element testas och fungerar oberoende av varandra. Varaktigheten av tiden (i timmar) för felfri drift av element har en fördelningsdensitetsfunktion: för det första: F 1 (t) =1-e- 0,1 t, för det andra: F 2 (t) = 1-e- 0,2 t, för den tredje: F 3 (t) =1-e- 0,3 t. Hitta sannolikheten att i tidsintervallet från 0 till 5 timmar: endast ett element kommer att misslyckas; endast två element kommer att misslyckas; alla tre elementen kommer att misslyckas.

Lösning: Låt oss använda definitionen av den sannolikhetsgenererande funktionen:

Sannolikheten att i oberoende försök, i den första av vilka sannolikheten för att en händelse inträffar A lika med , i den andra, etc. händelse A visas exakt en gång, lika med koefficienten i expansionen av genereringsfunktionen i potenser . Låt oss hitta sannolikheterna för misslyckande respektive icke-misslyckande för det första, andra och tredje elementet i tidsintervallet från 0 till 5 timmar:

Låt oss skapa en genererande funktion:

Koefficienten vid är lika med sannolikheten för att händelsen A kommer att visas exakt tre gånger, det vill säga sannolikheten för misslyckande för alla tre element; koefficienten vid är lika med sannolikheten att exakt två element kommer att misslyckas; koefficienten vid är lika med sannolikheten att endast ett element kommer att misslyckas.

Exempel 2.7. Givet sannolikhetstätheten f(x)slumpvariabel X:

Hitta fördelningsfunktionen F(x).

Lösning: Vi använder formeln:

.

Således ser distributionsfunktionen ut så här:

Exempel 2.8. Enheten består av tre oberoende verksamma element. Sannolikheten för misslyckande för varje element i ett experiment är 0,1. Gör upp en distributionslag för antalet misslyckade element i ett experiment.

Lösning: Slumpmässigt värde X– antalet element som misslyckades i ett experiment – ​​kan ha följande värden: 0, 1, 2, 3. Sannolikheter som X tar dessa värden, finner vi att använda Bernoullis formel:

Således får vi följande lag för sannolikhetsfördelning av en slumpvariabel X:

Exempel 2.9. I en sats om 6 delar finns det 4 standarddelar. 3 delar valdes ut slumpmässigt. Gör upp en distributionslag för antalet standarddelar bland de utvalda.

Lösning: Slumpmässigt värde X– antalet standarddelar bland de valda – kan ha följande värden: 1, 2, 3 och har en hypergeometrisk fördelning. Sannolikheter att X

Var -- antal delar i partiet;

-- antal standarddelar i en batch;

– antal valda delar;

-- antal standarddelar bland de valda.

.

.

.

Exempel 2.10. Slumpvariabeln har en distributionstäthet

och är inte kända, men , a och . Hitta och.

Lösning: I det här fallet den slumpmässiga variabeln X har en triangulär fördelning (Simpson-fördelning) på intervallet [ a, b]. Numeriska egenskaper X:

Därav, . När vi löser detta system får vi två värdepar: . Eftersom vi enligt villkoren för problemet äntligen har: .

Svar: .

Exempel 2.11. I genomsnitt, under 10 % av avtalen, betalar försäkringsbolaget försäkringsbelopp i samband med att ett försäkringsfall inträffar. Beräkna den matematiska förväntan och spridningen av antalet sådana kontrakt bland fyra slumpmässigt utvalda.

Lösning: Den matematiska förväntningen och variansen kan hittas med hjälp av formlerna:

.

Möjliga värden för SV (antal kontrakt (av fyra) vid inträffandet av ett försäkringsfall): 0, 1, 2, 3, 4.

Vi använder Bernoullis formel för att beräkna sannolikheterna för olika antal kontrakt (av fyra) för vilka försäkringsbeloppen betalades:

.

IC-distributionsserien (antal kontrakt med inträffandet av en försäkringsfall) har formen:

	0,6561	0,2916	0,0486	0,0036	0,0001

Svar: , .

Exempel 2.12. Av de fem rosorna är två vita. Rita upp en fördelningslag för en slumpvariabel som uttrycker antalet vita rosor bland två som tas samtidigt.

Lösning: I ett urval av två rosor kan det antingen inte finnas någon vit ros, eller så kan det finnas en eller två vita rosor. Därför den slumpmässiga variabeln X kan ta värden: 0, 1, 2. Sannolikheter att X tar dessa värden, hittar vi det med formeln:

Var -- antal rosor;

-- antal vita rosor;

– antal rosor tagna samtidigt;

-- antalet vita rosor bland de tagna.

.

.

.

Då kommer distributionslagen för den slumpmässiga variabeln att vara följande:

Exempel 2.13. Bland de 15 monterade enheterna kräver 6 ytterligare smörjning. Gör upp en distributionslag för antalet enheter som behöver ytterligare smörjning bland fem slumpmässigt utvalda från det totala antalet.

Lösning: Slumpmässigt värde X– antalet enheter som kräver ytterligare smörjning bland de fem valda – kan ta följande värden: 0, 1, 2, 3, 4, 5 och har en hypergeometrisk fördelning. Sannolikheter att X tar dessa värden, hittar vi det med formeln:

Var -- antal sammansatta enheter;

-- antalet enheter som kräver ytterligare smörjning;

– antal utvalda enheter;

-- antalet enheter som kräver ytterligare smörjning bland de valda.

.

.

.

.

.

.

Då kommer distributionslagen för den slumpmässiga variabeln att vara följande:

Exempel 2.14. Av de 10 klockor som tagits emot för reparation kräver 7 allmän rengöring av mekanismen. Klockorna är inte sorterade efter typ av reparation. Mästaren, som vill hitta klockor som behöver rengöras, undersöker dem en efter en och efter att ha hittat sådana klockor slutar han att titta på dem. Hitta den matematiska förväntningen och variansen för antalet tittade timmar.

Lösning: Slumpmässigt värde X– antalet enheter som behöver ytterligare smörjning bland de fem valda – kan ta följande värden: 1, 2, 3, 4. Sannolikheter för att X tar dessa värden, hittar vi det med formeln:

.

.

.

.

Då kommer distributionslagen för den slumpmässiga variabeln att vara följande:

Låt oss nu beräkna de numeriska egenskaperna för kvantiteten:

Svar: , .

Exempel 2.15. Prenumeranten har glömt den sista siffran i telefonnumret han behöver, men kommer ihåg att det är udda. Hitta den matematiska förväntningen och variansen av antalet gånger han slår ett telefonnummer innan han når det önskade numret, om han slår den sista siffran slumpmässigt och inte därefter slår den slagna siffran.

Lösning: Slumpvariabeln kan ha följande värden: . Eftersom abonnenten inte slår den slagna siffran i framtiden, är sannolikheten för dessa värden lika.

Låt oss sammanställa en distributionsserie av en slumpvariabel:

	0,2

Låt oss beräkna den matematiska förväntan och variansen för antalet uppringningsförsök:

Svar: , .

Exempel 2.16. Sannolikheten för fel under tillförlitlighetstestning för varje enhet i serien är lika med sid. Bestäm den matematiska förväntningen på antalet enheter som misslyckades om de testades N enheter.

Lösning: Diskret slumpvariabel X är antalet felaktiga enheter i N oberoende test, i var och en av vilka sannolikheten för misslyckande är lika stor p, fördelade enligt binomiallagen. Den matematiska förväntan på en binomialfördelning är lika med antalet försök multiplicerat med sannolikheten för att en händelse inträffar i ett försök:

Exempel 2.17. Diskret slumpvariabel X tar 3 möjliga värden: med sannolikhet ; med sannolikhet och med sannolikhet. Hitta och , med vetskap om att M( X) = 8.

Lösning: Vi använder definitionerna av matematisk förväntan och distributionslagen för en diskret slumpvariabel:

Vi hittar: .

Exempel 2.18. Den tekniska kontrollavdelningen kontrollerar produkternas standard. Sannolikheten att produkten är standard är 0,9. Varje batch innehåller 5 produkter. Hitta den matematiska förväntan av en slumpvariabel X– antalet partier, som var och en innehåller exakt 4 standardprodukter, om 50 partier är föremål för kontroll.

Lösning: I det här fallet är alla utförda experiment oberoende, och sannolikheterna för att varje sats innehåller exakt 4 standardprodukter är desamma, därför kan den matematiska förväntningen bestämmas med formeln:

,

var är antalet parter;

Sannolikheten att en batch innehåller exakt 4 standardprodukter.

Vi hittar sannolikheten med Bernoullis formel:

Svar: .

Exempel 2.19. Hitta variansen för en slumpvariabel X– antal händelser av händelsen A i två oberoende försök, om sannolikheten för att en händelse inträffar i dessa försök är densamma och det är känt att M(X) = 0,9.

Lösning: Problemet kan lösas på två sätt.

1) Möjliga värden för SV X: 0, 1, 2. Med hjälp av Bernoullis formel bestämmer vi sannolikheterna för dessa händelser:

, , .

Sedan distributionslagen X har formen:

Från definitionen av matematisk förväntan bestämmer vi sannolikheten:

Låt oss hitta spridningen av SV X:

.

2) Du kan använda formeln:

.

Svar: .

Exempel 2.20. Förväntning och standardavvikelse för en normalfördelad stokastisk variabel X lika med 20 respektive 5. Hitta sannolikheten att som ett resultat av testet X kommer att ta värdet i intervallet (15; 25).

Lösning: Sannolikhet att träffa en normal slumpvariabel X på avsnittet från till uttrycks genom Laplace-funktionen:

Exempel 2.21. Given funktion:

Vid vilket parametervärde C denna funktion är fördelningsdensiteten för någon kontinuerlig slumpvariabel X? Hitta den matematiska förväntan och variansen för en slumpvariabel X.

Lösning: För att en funktion ska vara fördelningsdensiteten för någon slumpvariabel måste den vara icke-negativ och den måste uppfylla egenskapen:

.

Därav:

Låt oss beräkna den matematiska förväntan med formeln:

.

Låt oss beräkna variansen med formeln:

T är lika sid. Det är nödvändigt att hitta den matematiska förväntan och variansen för denna slumpvariabel.

Lösning: Fördelningslagen för en diskret slumpvariabel X - antalet förekomster av en händelse i oberoende försök, i var och en av vilka sannolikheten för att händelsen inträffar är lika med , kallas binomial. Den matematiska förväntan på binomialfördelningen är lika med produkten av antalet försök och sannolikheten för att händelse A inträffar i ett försök:

.

Exempel 2.25. Tre oberoende skott avlossas mot målet. Sannolikheten att träffa varje skott är 0,25. Bestäm standardavvikelsen för antalet träffar med tre skott.

Lösning: Eftersom tre oberoende försök utförs, och sannolikheten för att händelse A (en träff) inträffar i varje försök är densamma, kommer vi att anta att den diskreta slumpvariabeln X - antalet träffar på målet - fördelas enligt binomial lag.

Variansen av binomialfördelningen är lika med produkten av antalet försök och sannolikheten för att en händelse inträffar och uteblir i ett försök:

Exempel 2.26. Det genomsnittliga antalet kunder som besöker ett försäkringsbolag på 10 minuter är tre. Hitta sannolikheten för att minst en klient kommer att anlända inom de närmaste 5 minuterna.

Genomsnittligt antal kunder som anländer inom 5 minuter: . .

Exempel 2.29. Väntetiden för en applikation i processorkön följer en exponentiell distributionslag med ett medelvärde på 20 sekunder. Hitta sannolikheten att nästa (slumpmässiga) begäran kommer att vänta på processorn i mer än 35 sekunder.

Lösning: I detta exempel, den matematiska förväntan , och felfrekvensen är lika med .

Sedan önskad sannolikhet:

Exempel 2.30. En grupp på 15 elever håller möte i en sal med 20 rader med vardera 10 platser. Varje elev tar plats i hallen slumpmässigt. Hur stor är sannolikheten att inte fler än tre personer hamnar på sjunde plats i raden?

Lösning:

Exempel 2.31.

Sedan, enligt den klassiska definitionen av sannolikhet:

Var -- antal delar i partiet;

-- antal icke-standardiserade delar i partiet;

– antal valda delar;

-- antal icke-standarddelar bland de valda.

Då blir den slumpmässiga variabelns fördelningslag följande.

Matematisk förväntan diskret slumpvariabel kallas:

I fallet med en oändlig uppsättning värden finns det en serie på höger sida av (4.4), och vi kommer endast att överväga de värden av X för vilka denna serie är absolut konvergent.

M(X) representerar det genomsnittliga förväntade värdet för en slumpvariabel. Den har följande egenskaper:

1) M(C)=C, där C=konst

2) M (CX)=CM (X) (4,5)

3) M (X+Y)=M(X)+M(Y), för alla X och Y.

4) M (XY)=M (X)M(Y), om X och Y är oberoende.

Att uppskatta graden av spridning av värdena för en slumpvariabel runt dess medelvärde M(X)= A begrepp introduceras avvikelserD(X) och medelkvadrat (standard)avvikelse. Variation kallas den matematiska förväntan av den kvadratiska skillnaden (X-), de där. :

D(X)=M(X-)2 = pi,

Var =M(X); definieras som kvadratroten av variansen, dvs. .

För att beräkna variansen använd formeln:

(4.6)

Dispersionsegenskaper och standardavvikelse:

1) D(C)=0, där C=konst

2) D(CX)=C2D(X), (CX)= çCç (X) (4.7)

3) D(X+Y) =D(X)+D(Y),

om X och Y är oberoende.

Storheternas dimension och sammanfaller med dimensionen av den slumpmässiga variabeln X själv, och dimensionen på D(X) är lika med kvadraten på dimensionen av den slumpmässiga variabeln X.

4.3. Matematiska operationer på slumpvariabler.

Låt slumpvariabeln X ta värden med sannolikheter och slumpvariabeln Y ta värden med sannolikheter. Produkten KX av slumpvariabeln X och konstantvärdet K är en ny slumpvariabel som med samma sannolikheter som slumpen variabel X, tar värden lika med produkterna med K-värden för den slumpmässiga variabeln X. Följaktligen har dess distributionslag formen Tabell 4.2:

Tabell 4.2

			...
			...

Fyrkant slumpvariabel X, dvs. , är en ny slumpvariabel som, med samma sannolikheter som slumpvariabeln X, tar värden lika med kvadraterna på dess värden.

Belopp slumpvariablerna X och Y är en ny slumpvariabel som tar alla värden av formen med sannolikheter som uttrycker sannolikheten att slumpvariabeln X tar värdet och Y är värdet, dvs.

(4.8)

Om slumpvariablerna X och Y är oberoende, då:

Skillnaden och produkten av stokastiska variabler X och Y bestäms på liknande sätt.

Skillnad slumpvariabler X och Y - detta är en ny slumpvariabel som tar alla värden i formen och arbete- alla värden i formen med sannolikheter bestämda av formeln (4.8), och om de slumpmässiga variablerna X och Y är oberoende, då av formeln (4.9).

4.4. Bernoulli och Poisson distributioner.

Betrakta en sekvens av n identiska upprepade försök som uppfyller följande villkor:

1. Varje test har två resultat, som kallas framgång och misslyckande.

Dessa två utfall är ömsesidigt oförenliga och motsatta händelser.

2. Sannolikheten för framgång, betecknad p, förblir konstant från försök till försök. Sannolikheten för misslyckande betecknas med q.

3. Alla n tester är oberoende. Detta innebär att sannolikheten för att en händelse inträffar i någon av n upprepade försök inte beror på resultaten från andra försök.

Sannolikheten att i n oberoende upprepade försök, i var och en av vilka sannolikheten för att en händelse inträffar är lika med , kommer händelsen att inträffa exakt m gånger (i valfri sekvens) är lika med

(4.10)

Uttryck (4.10) kallas Bernoullis formel.

Sannolikheter för att händelsen inträffar:

a) mindre än m gånger,

b) mer än m gånger,

c) minst m gånger,

d) inte mer än m gånger - hittas i enlighet med formlerna:

Binomial är lagen för distribution av en diskret slumpvariabel X - antalet förekomster av en händelse i n oberoende försök, i var och en av vilka sannolikheten för att händelsen inträffar är lika med p; sannolikheterna för möjliga värden X = 0,1,2,..., m,...,n beräknas med Bernoullis formel (tabell 4.3).

Tabell 4.3

Antal framgångar X=m				...	m	...	n
Sannolikhet P				...		...

Eftersom den högra sidan av formeln (4.10) representerar den allmänna termen för binomialexpansionen, kallas denna fördelningslag binom. För en stokastisk variabel X fördelad enligt binomiallagen har vi.